常规的整数划分
考虑对一个正整数 N 划分为若干个正整数的和,求所有方案数。
如当 ![]() 时,所有的方案(共 7 种)如下:5、4 + 1、3 + 2、3 + 1 + 1、2 + 2 + 1、2 + 1 + 1 + 1、1 + 1 + 1 + 1 + 1。
时,所有的方案(共 7 种)如下:5、4 + 1、3 + 2、3 + 1 + 1、2 + 2 + 1、2 + 1 + 1 + 1、1 + 1 + 1 + 1 + 1。
不难想出解决这个问题的一个有效方法是动态规划(分治法)。
若定义 ![]() 为正整数
为正整数 ![]() 划分为若干正整数的和的所有方案数,会发现我们很难仅从
划分为若干正整数的和的所有方案数,会发现我们很难仅从 ![]() 去推导出
去推导出 ![]() ,事实上
,事实上 ![]() 与
与 ![]() 均有关系。
均有关系。
一个合理的思路是,先取定一个加数 ![]() ,然后可以立即得到一个方案:
,然后可以立即得到一个方案:
![]()
如何从上式推出更多方案呢?可以对![]() 继续划分,如固定一个加数
继续划分,如固定一个加数 ![]() ,同理得到
,同理得到 ![]() ,那么就能得到
,那么就能得到 ![]() 的另一个方案:
的另一个方案:
![]()
这样便可以将问题规模逐渐变小。当然这个思路是比较粗略的,原因在于目前这种定义的结构没有序:如果对固定的加数进行遍历,会重复计算相同的方案数(如 5 = 2 + 3 = 3 + 2),并且由于大量相同子问题的重复计算,时间复杂度也是很高的。
为了增加有序性,我们采用二维数组定义,定义![]() 为正整数 i 划分为若干不大于
为正整数 i 划分为若干不大于 ![]() 的正整数的和的所有方案数。在这个定义下,问题的答案即
的正整数的和的所有方案数。在这个定义下,问题的答案即 ![]() ,并且很容易得到状态转移方程。
,并且很容易得到状态转移方程。
先考虑特殊情况,假如要计算一个 ![]() ,显然,按定义,不能存在大于
,显然,按定义,不能存在大于 ![]() 的加数。那么可分为下面两种情形:
的加数。那么可分为下面两种情形:
- 若存在加数
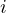 ,则只有一种划分,即
,则只有一种划分,即  ,方案数为1
,方案数为1 - 若不存在加数
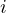 ,即所有加数都不大于
,即所有加数都不大于  ,此时方案数即为
,此时方案数即为 ![Rendered by QuickLaTeX.com dp[i, i - 1]](http://43.136.110.234/wp-content/ql-cache/quicklatex.com-3e2f095c6fc705c5280769101a0dac0d_l3.png)
即当 ![]() 时,我们有
时,我们有 ![]()
当 ![]() 时,由于加数不能为负数,我们有
时,由于加数不能为负数,我们有 ![]()
当 ![]() 时
时
- 若存在加数
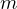 ,
, 则此时划分等价于对
则此时划分等价于对 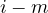 进行加数不大于
进行加数不大于 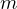 的划分,方案数为
的划分,方案数为![Rendered by QuickLaTeX.com dp[i - m, m]](http://43.136.110.234/wp-content/ql-cache/quicklatex.com-61aa89d1128412a5ed5778599337560e_l3.png)
- 若不存在加数
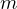 ,此时相当于对
,此时相当于对 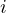 进行加数不大于
进行加数不大于  的划分,这恰好符合 dp 的定义:
的划分,这恰好符合 dp 的定义:![Rendered by QuickLaTeX.com dp[i , m - 1]](http://43.136.110.234/wp-content/ql-cache/quicklatex.com-20ab9996db8574ebdc61eafdf441351d_l3.png) 必定不含加数
必定不含加数 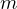 ,即此时方案数为
,即此时方案数为 ![Rendered by QuickLaTeX.com dp[i, m - 1]](http://43.136.110.234/wp-content/ql-cache/quicklatex.com-743a1314c8bda8f9eb82251e5042256f_l3.png)
即当 ![]() 时,我们有
时,我们有 ![]()
综上,状态转移方程为:
![Rendered by QuickLaTeX.com \[dp[i, m]= \begin{cases} dp[i, i],\quad &m > i \\ 1 + dp[i, i - 1],\quad &m= i \\ dp[i - m, m] + dp[i, m - 1],\quad &m < i \end{cases}\]](http://43.136.110.234/wp-content/ql-cache/quicklatex.com-79d5c557c73025687eee0d6a91a96f8f_l3.png)
再考虑边界条件,1 只有一种划分,即1 = 1。且对任意正整数 i,加数不大于 1 的划分也只有一种,即 i 个 1 相加。边界条件为![]() 和
和![]()
C语言实现:
unsigned q(unsigned n, unsigned m)
{
int dp[n + 1][m + 1];
memset(dp, -1, sizeof(dp));
for(int i = 1; i <= n; i++)
{
dp[i][1] = 1;
}
for(int i = 1; i <= m; i++)
{
dp[1][i] = 1;
}
for(int i = 2; i <= n; i++)
{
for(int j = 2; j <= m; j++)
{
if(j > i) dp[i][j] = dp[i][i];
else if(j == i) dp[i][j] = dp[i][i - 1] + 1;
else dp[i][j] = dp[i][j - 1] + dp[i - j][j];
}
}
//printArray2D(dp, n + 1, m + 1);
return dp[n][m];
}
接下来解决这个问题的一些变体。
K个加数的划分
若规定分解的加数必须为![]() 个,那么计数的范围就减少了。一个直观的思路是依旧使用上面的划分方法,但是过滤掉加数个数不为
个,那么计数的范围就减少了。一个直观的思路是依旧使用上面的划分方法,但是过滤掉加数个数不为![]() 的分解,但这样的话会有些麻烦。由于限定加数个数后,问题依旧具有最优子结构性质,我们还是可以通过动态规划的方式去解决,区别只是状态数组的定义和状态转移方程不同而已。
的分解,但这样的话会有些麻烦。由于限定加数个数后,问题依旧具有最优子结构性质,我们还是可以通过动态规划的方式去解决,区别只是状态数组的定义和状态转移方程不同而已。
举例:当![]() 时,共有3 + 1 + 1、2 + 2 + 1两种。
时,共有3 + 1 + 1、2 + 2 + 1两种。
依旧采用二维数组,定义![]() 为正整数 i 划分为
为正整数 i 划分为![]() 个正整数的和的所有方案数。在这个定义下,问题的答案即
个正整数的和的所有方案数。在这个定义下,问题的答案即 ![]() 。接下来考虑状态转移:
。接下来考虑状态转移:
- 若
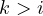 ,由于加数都是正整数,这样的划分不存在。方案数为0。
,由于加数都是正整数,这样的划分不存在。方案数为0。 - 若
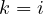 ,这样的划分只有一种,即 k 个 1 相加。方案数为1。
,这样的划分只有一种,即 k 个 1 相加。方案数为1。 - 若
 ,依旧分为两种情形
,依旧分为两种情形
- 若加数恰好全不为1,即先分配 k 个 1 作为所有的加数(由于
 ,这样的分配总是可行的),再将余下的
,这样的分配总是可行的),再将余下的 分配到这 k 个 1 上面,方案数为
分配到这 k 个 1 上面,方案数为 ![Rendered by QuickLaTeX.com dp[i-k,k]](http://43.136.110.234/wp-content/ql-cache/quicklatex.com-0c2d52368bd1a2dfcd945f00a90d617c_l3.png) 。注意这种情形方案数可能为0
。注意这种情形方案数可能为0 - 若加数存在至少一个1,即先固定一个加数为1,再将余下的
 分解为
分解为 个加数,方案数为
个加数,方案数为![Rendered by QuickLaTeX.com dp[i - 1, k - 1]](http://43.136.110.234/wp-content/ql-cache/quicklatex.com-c41a83d8c7872a1e973dc4fb5b239ed1_l3.png)
- 若加数恰好全不为1,即先分配 k 个 1 作为所有的加数(由于
即可以得到如下的状态转移方程:
![Rendered by QuickLaTeX.com \[dp[i, k]= \begin{cases} 0,\quad &k > i \\ 1,\quad &k = i \\ dp[i - k, k] + dp[i - 1, k - 1],\quad &k < i \end{cases}\]](http://43.136.110.234/wp-content/ql-cache/quicklatex.com-4d3690641b8ad5fe4dede13c0fcf46b5_l3.png)
再考虑边界条件,显然有![]() 和
和![]()
C语言实现:
unsigned q_k(unsigned n, unsigned k)
{
int dp[n + 1][k + 1];
memset(dp, -1, sizeof(dp));
for(int i = 1; i <= n; i++)
{
dp[i][1] = 1;
}
for(int i = 2; i <= k; i++)
{
dp[1][i] = 0;
}
for(int i = 2; i <= n; i++)
{
for(int j = 2; j <= k; j++)
{
if(j > i) dp[i][j] = 0;
else if(j == i) dp[i][j] = 1;
else dp[i][j] = dp[i - j][j] + dp[i - 1][j - 1];
}
}
return dp[n][k];
}
最多K个加数的划分
若规定加数最多为![]() 个,也可通过改变定义来求解。定义
个,也可通过改变定义来求解。定义![]() 为正整数 i 划分为最多
为正整数 i 划分为最多![]() 个正整数的和的所有方案数。在这个定义下,问题的答案即
个正整数的和的所有方案数。在这个定义下,问题的答案即 ![]() 。
。
- 若
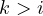 ,
,![Rendered by QuickLaTeX.com dp[i, k] = dp[i, i]](http://43.136.110.234/wp-content/ql-cache/quicklatex.com-074f770900b7226565365839e92df597_l3.png)
- 若
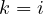 ,
,![Rendered by QuickLaTeX.com dp[i, k] = 1 + dp[i, i - 1]](http://43.136.110.234/wp-content/ql-cache/quicklatex.com-b52b7b011e2bc43681bb10d10f969092_l3.png)
- 若
 ,依旧分为两种情形
,依旧分为两种情形
- 若加数恰好有
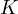 个,即先分配 k 个 1 作为所有的加数(由于
个,即先分配 k 个 1 作为所有的加数(由于 ,这样的分配总是可行的),再将余下的
,这样的分配总是可行的),再将余下的 分配到这 k 个 1 上面,方案数为
分配到这 k 个 1 上面,方案数为 ![Rendered by QuickLaTeX.com dp[i-k,k]](http://43.136.110.234/wp-content/ql-cache/quicklatex.com-0c2d52368bd1a2dfcd945f00a90d617c_l3.png) 。注意这种情形方案数可能为0
。注意这种情形方案数可能为0 - 若加数最多只有
 个,方案数为
个,方案数为![Rendered by QuickLaTeX.com dp[i, k - 1]](http://43.136.110.234/wp-content/ql-cache/quicklatex.com-594e8c48b1a80567a205267a8f0872f4_l3.png)
- 若加数恰好有
状态转移方程为:
![Rendered by QuickLaTeX.com \[dp[i, k]= \begin{cases} dp[i, i],\quad &k > i \\ 1 + dp[i, i - 1],\quad &k = i \\ dp[i - k, k] + dp[i, k - 1],\quad &k < i \end{cases}\]](http://43.136.110.234/wp-content/ql-cache/quicklatex.com-de2f51a682003a1efeb636b8a1ba526c_l3.png)
注意到这个转移方程和常规情形竟然是一致的,甚至边界条件也是相同的。边界条件为![]() 和
和![]() 。这说明使用动态规划解决背景不同的两个问题时,可能具有相同的结构!
。这说明使用动态规划解决背景不同的两个问题时,可能具有相同的结构!
具体到这个例子上,对正整数 ![]() 进行划分,所有加数均不大于
进行划分,所有加数均不大于![]() 的划分方案数和加数个数不大于
的划分方案数和加数个数不大于![]() 的划分方案数总是相等的。如
的划分方案数总是相等的。如![]() 时
时
- 所有加数均不大于
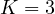 ,有3 + 2、3 + 1 + 1、2 + 2 + 1、2 + 1 + 1 + 1、1 + 1 + 1 + 1 + 1共5种
,有3 + 2、3 + 1 + 1、2 + 2 + 1、2 + 1 + 1 + 1、1 + 1 + 1 + 1 + 1共5种 - 加数个数不大于
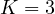 ,有5、4 + 1、3 + 2、3 + 1 + 1、2 + 2 + 1共5种
,有5、4 + 1、3 + 2、3 + 1 + 1、2 + 2 + 1共5种
C语言实现:
unsigned q_maxk(unsigned n, unsigned k)
{
int dp[n + 1][k + 1];
memset(dp, -1, sizeof(dp));
for(int i = 1; i <= n; i++)
{
dp[i][1] = 1;
}
for(int i = 1; i <= k; i++)
{
dp[1][i] = 1;
}
for(int i = 2; i <= n; i++)
{
for(int j = 2; j <= k; j++)
{
if(j > i) dp[i][j] = dp[i][i];
else if(j == i) dp[i][j] = dp[i][i - 1] + 1;
else dp[i][j] = dp[i][j - 1] + dp[i - j][j];
}
}
return dp[n][k];
}
相异加数的划分
若规定加数不能相同,反而会比上面两种变体更简单些,只需对常规情形进行一点修改即可。定义![]() 为正整数 i 划分为相异且不超过
为正整数 i 划分为相异且不超过![]() 的正整数的和的所有方案数。在这个定义下,问题的答案即
的正整数的和的所有方案数。在这个定义下,问题的答案即 ![]() 。
。
容易得到状态转移方程:
![Rendered by QuickLaTeX.com \[dp[i, m]= \begin{cases} dp[i, i],\quad &m > i \\ 1 + dp[i, i - 1],\quad &m = i \\ dp[i - m, m - 1] + dp[i, m - 1],\quad &m< i \end{cases}\]](http://43.136.110.234/wp-content/ql-cache/quicklatex.com-38352e36d96aceabcda38257a429c229_l3.png)
C语言实现:
unsigned q_unique(unsigned n, unsigned m)
{
int dp[n + 1][m + 1];
memset(dp, -1, sizeof(dp));
for(int i = 1; i <= m; i++)
{
dp[1][i] = 1;
}
for(int i = 2; i <= n; i++)
{
dp[i][1] = 0;
}
for(int i = 2; i <= n; i++)
{
for(int j = 2; j <= m; j++)
{
if(j > i) dp[i][j] = dp[i][i];
else if(j == i) dp[i][j] = dp[i][i - 1] + 1;
else dp[i][j] = dp[i][j - 1] + dp[i - j][j - 1];
}
}
return dp[n][m];
}
